Two different waves with the same frequency and wavelengths can be coupled, so that the amplitude alternates periodically between the two to form a phenomenon known as a coherent beating oscillation. The process can be observed often with a coupled pendulum, and at the cosmic scale as neutrino oscillations that occur due to fluctuations between diverse neutrinos. Solids too can equally maintain various wave excitations to contribute to their thermal and electromagnetic properties.
In a new report now published in Nature Communications Physics, Tomosato Hioki and a team of scientists in materials research and applied physics at the Tohoku University and the University of Tokyo in Japan, described coherent beating observed between different excitation species in a solid, namely phonons—quantum vibrational mechanical energy, and magnons—a quasiparticle representing the collective excitation of the electron’s spin structure. The team used time-resolved magneto-optical microscopy to show how magnons generated in a compound gradually disappeared by transferring to phonons, to then return to the form of magnons after a while. The oscillation period was consistent with magnon-phonon beating. The scientists envision the experimental outcomes will pave way to coherently control magnon-phonon systems in solids.
Phonon-magnon interactions in lutetium iron garnet
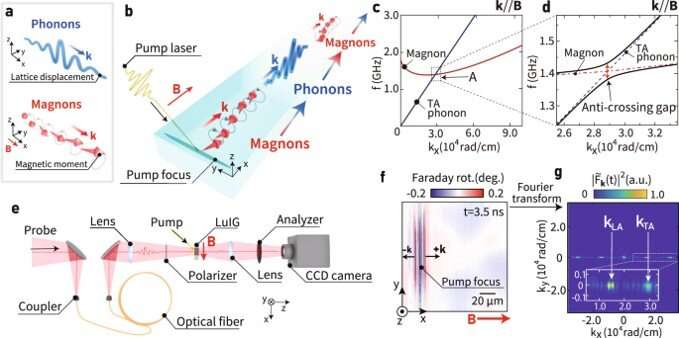
Phonons are vibrational waves of a solid crystal lattice responsible for the elasticity and thermal properties of solids. Magnons or spin waves are conversely representative of a wavy motion of magnetization, present in magnets responsible for their magnetic and thermal properties. These two particles can interact within solids via magneto-elastic and magneto-static couplings. The dynamics of the particles are provided in the dispersion curves of each system to show the relationship between the wave number and frequency. Scientists have recorded the dispersion curves of transverse acoustic phonons and magnons in a film of a typical insulator such as lutetium iron garnet. Such dispersion curves of the phonon and magnon particles maintain an intersection around which a magnon-phonon hybridized state can be formed. Researchers have found this state, to exhibit an extremely long lifetime, far greater than pure magnons due to hybridization with phonons that maintain a long lifetime.
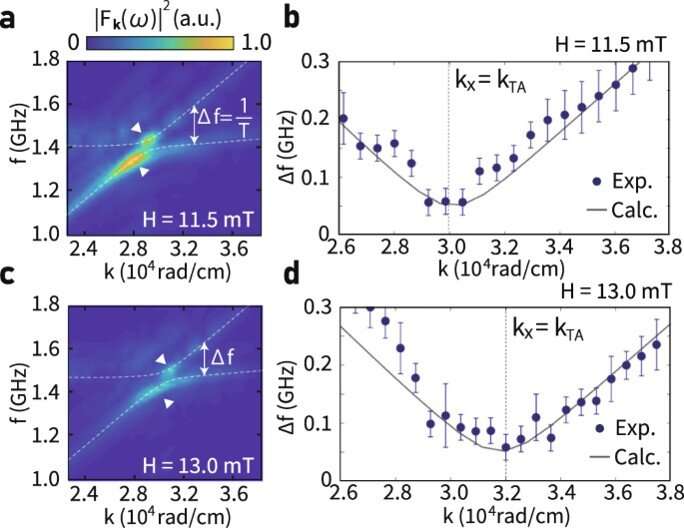
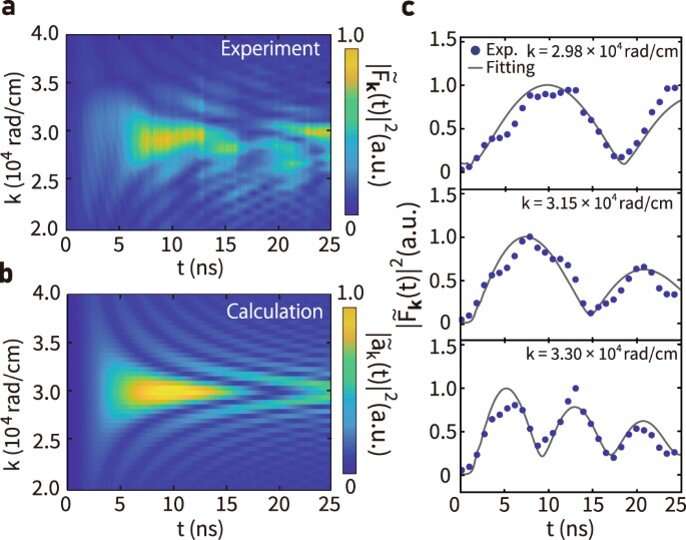
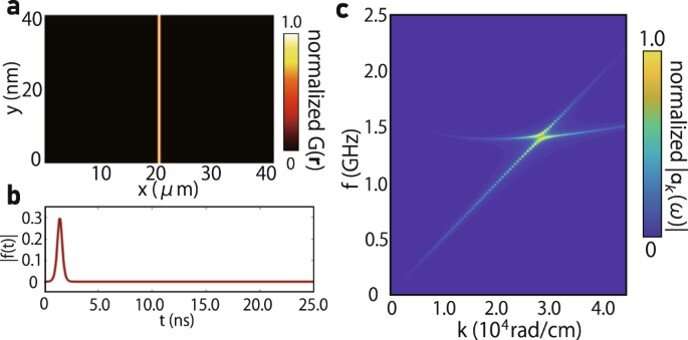
![Observation of magnon-phonon coherent oscillation. (a) Temporal evolution of the real part of F~k(t) at kx = kTA under the magnetic field B = 11.5 mT parallel to k, where kTA refers to the wavenumber of the intersection point between dispersion relations of transverse acoustic (TA) phonons and magnons. Red inverted triangles indicates t = 15 ns, 20 ns, and 25 ns after the pump pulse irradiation. (b) A frequency power spectrum of F~k(t) at kx = kTA. The blue filled circles represents experimentally obtained spectrum intensity, while the gray curve represents fitting curve. Inverted red triangle highlights peaks. Errors of the data are evaluated as a standard deviation, which is smaller than the data plot. (c) Theoretically calculated dispersion curves of magnon polarons around kx = kTA and ky = 0, where we use the crystalline anisotropy energy Kc = 73.0 [J ⋅ m−3], uniaxial anisotropy energy Ku = −767.5 [J ⋅ m−3], saturation magnetization Ms = 14.8 [kA ⋅ m−1], velocity of LA phonons vLA = 6.51 [km ⋅ s−1], velocity of TA phonons vTA = 3.06 [km ⋅ s−1] and magnon-phonon coupling constant b2 = 1.8 × 105 [J ⋅ m−3]. The black solid curves represent the dispersion curves of magnon polarons, while the blue and red dashed curves represent pure TA phonons and magnons, respectively. (d) Temporal evolution of the real part of F~k(t) at kx = kLA under the magnetic field B = 11.5 mT parallel to k, where kLA refers to the wavenumber of the intersection point between dispersion relations of longitudinal acoustic (LA) phonons and magnons. (e) A frequency power spectrum of F~k(t) at kx = kLA. The black filled circles represents experimentally obtained spectrum intensity, while the gray curve represents fitting curve. Errors of the data are evaluated as a standard deviation, which is smaller than the data plot. (f) Theoretically calculated dispersion curves of magnon polarons around kx = kLA. The gray line and red curve represent the dispersion curves of LA phonons and magnons, respectively. (g) Temporal evolution of the real part of F~k(t) at kx = kTA under the magnetic field B = 11.5 mT perpendicular to k. (h) Temporal evolution of real part of F~k(t) at kx = kLA under the magnetic field B = 11.5 mT perpendicular to k. (i), Magneto-optical images taken at different delay times. Credit: <i>Communications Physics</i> (2022). DOI: 10.1038/s42005-022-00888-1 Coherent oscillation between phonons and magnons](https://scx1.b-cdn.net/csz/news/800a/2022/coherent-oscillation-b-1.jpg)
Physicists have confirmed the extended lifetime in lutetium iron garnet, while measuring the spin-heat conversion, even at room temperature. The researchers expect to simultaneously observe a coherent superposition that forms a corresponding beating oscillation between phonons and magnons. In this work, Hioki et al described the observation of coherent beating between two phonons and magnons within lutetium iron garnet. The team used time-resolved magneto-optical microscopy and measured the magnetization dynamics. They found the coherent beating of up to tens of nanoseconds, and experimentally confirmed strong coupling between magnons and phonons in the bare film of lutetium iron garnet, abbreviated as LUIG.
The experimental setup
Hioki et al explored the beating oscillations in solids by developing the time-resolved magneto-optical microscope. During the experiments, they used a thin film of LUIG with a thickness of 1.8 µm, with large magneto-optical effects and small magnetization damping. The team excited the magnetization dynamics by focusing a pulsed laser light with an 800 nm wavelength into the sample, which corresponded to almost half the energy of the bandgap of LUIG. The pump excited the spin wave or magnons via photo-induced de-magnetization and photo-induced expansion. The scientists selectively excited the magnon perpendicular to the vertical line by using Huygens-Fresnel interferences. Thereafter, they used another weak light pulse, known as the probe pulse on the sample with a wavelength of 630 nm, and measured the spatial distribution of the magneto-optical Faraday rotation of the probe pulse transmitted through the sample via a camera. The team resolved the magnon-phonon gap frequency in the sample during the experiments.
Coherent oscillations between phonons and magnons
The team obtained a polarization rotation angle after pump-pulse irradiation, where vertical wave patterns appeared in the vicinity of the focus of the pump pulse to demonstrate the magnon excitation of the device. They confirmed the polarization rotation to be due to the magneto-optical Faraday effect. The outcomes showed the development of magnon polarons at the intersection of the dispersion curves of magnons and phonons after pump-pulse irradiation. Hioki et al directly measured the pure magnons via microscopy to show the periodically oscillating signal as a function of time with the frequency of magnons.
They then measured the magneto-optical Faraday rotation and showed the disappearance of the signal when magnons transformed to phonons. The observed oscillations implied periodic beating between magnons and phonons in the time domain. The team further demonstrated the coherent beating oscillations in real-space via the timely change in the wave pattern excited by the pump pulse. They discussed the excitation spectra of magnons and coherent oscillation frequency, as well as the angular frequency at the intersection between magnon and phonon distribution curves. The outcomes showed good agreement with the theoretical calculations.
Outlook
In this way, Tomosato Hioki, and colleagues numerically measured the timely evolution of the magnon amplitude by computing the Fourier transform of the spectral magnon amplitude. The team considered the coupled dynamics between transverse acoustic phonons and magnons to be relevant to the observed oscillation. To understand the experimental outcomes, Hioki et al credited the large cooperativity to the small intrinsic magnetic damping, and high quality factor of phonons in garnet crystals. The scientists further enhanced the magnon-phonon coupling in the film by fabricating phononic or magnonic crystals out of the plane film, to aid the control of magnons in magnonic circuits and devices. The presented magnon-phonon coherent oscillations provide a platform to study the dynamics of coupled systems, to regulate the magnetic and elastic properties in a variety of magnetic materials.
Tomosato Hioki et al, Coherent oscillation between phonons and magnons, Communications Physics (2022). DOI: 10.1038/s42005-022-00888-1
L. J. Cornelissen et al, Long-distance transport of magnon spin information in a magnetic insulator at room temperature, Nature Physics (2015). DOI: 10.1038/nphys3465
© 2022 Science X Network
Citation:
Coherent oscillation between phonons and magnons (2022, May 30)
retrieved 30 May 2022
from https://phys.org/news/2022-05-coherent-oscillation-phonons-magnons.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no
part may be reproduced without the written permission. The content is provided for information purposes only.


